I Made Hundreds of Videos
Since 2007, I have created over 250 instructional videos for my online training site ScalaCourses.com. I built the web application that runs the site, wrote most of the content, and did all the videography.
I also create explanatory videos for court cases. This is helpful when complex and/or technical information needs to be presented.
Sample Explanatory Video
Following is an explanatory video that I created for a case, modified so that identifiable information is redacted, and with extra context added so that the video makes more sense to viewers who were not involved in the case. The information presented in this video is one aspect of the digital fingerprint of the ‘noise’ in the software that I discussed in the previous article.
Transcript
Hello, my name is Michael Slinn. This video has been prepared to explain one of the central concepts behind the opinions expressed in my report. At issue is whether the similarities in two bodies of code could be explained as a curious coincidence, or whether the likelihood of this being a random coincidence is extremely improbable. That would allow me to opine wether or not the author(s) of the second program must have accessed the first program so they could literally translate code written in the first computer language into a second computer language.
Question Addressed
The precise question that this video addresses is complex, and can be summarized as:
What is the improbability of 6 items appearing the in same order in two identical lists containing the same 26 items, after shuffling?
Concept: Factorial
This video shows the question visually, and also shows the answer in a compelling manner. In this video I demonstrate the likelihood of 26 routes found in both bodies of code, such that 6 of those routes appear in the same order in each program. This ‘co-incidence’ is approximately 2.5 times more unlikely than the chances that any two random humans have the same fingerprints. First, we need to understand a mathematical concept This concept is interesting and not difficult, I promise!
A factorial is mathematical shorthand. It is just a quick way of writing a tedious multiplication. Factorials are written as an exclamation mark (!) after a number. Let’s see some examples.
2! = 2 x 1 = 2
3! = 3 x 2 x 1 = 6
4! = 4 x 3 x 2 x 1 = 24
5! = 5 x 4 x 3 x 2 x 1 = 120
6! = 6 x 5 x 4 x 3 x 2 x 1 = 720
10! = 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 3,628,800
15! = 15 x 14 x 13 x 12 x 11 x 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1
= 1,307,674,368,000
(1.3 trillion)
20! = 20 x 19 x 18 x 17 x 16 x
15 x 14 x 13 x 12 x 11 x 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1
= 2,432,902,008,176,640,000
(about 2 quintillion, or 2 followed by 18 zeroes)
26! = 26 x 25 x 24 x 23 x 22 x 21 x 20 x 19 x 18 x 17 x 16 x
15 x 14 x 13 x 12 x 11 x 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1
= 403,291,461,126,605,635,584,000,000
(about 4 octillion, or 4 followed by 26 zeroes)
Analogy
- Start with a deck of cards.
- Remove half of them (take away 2 suits).
- 26 cards remain.
- Do the same with another deck of cards. Now you have 2 half decks, each of which has the same cards as the other.
- Shuffle both decks.
Let’s examine the odds of finding the same sequence of cards in both half-decks.
- What are the odds of finding 2 cards in the same sequence in both half-decks?
- Notice that the two sequences are in different locations in the deck. The topmost half-deck of cards has the sequence occurring about 2/3 of the way through that half-deck, whereas the bottom-most half-deck of cards has the sequence occurring hear the beginning of that half-deck.
- The equation for that probability is 26! / 24! = 1 : 650
- OK, what are the odds of finding 3 cards in the same sequence in both half-decks?
- The equation for that probability is 26! / 23! = 1 : 15,600
- Now let’s consider the odds of finding 4 cards in the same sequence in both half-decks.
- The equation for that probability is 26! / 22! = 1 : 358,800
- Next let’s consider the odds of finding 5 cards in the same sequence in both half-decks.
- The equation for that probability is 26! / 21! = 1 : 7,893,600
- Next let’s consider the odds of finding 6 cards in the same sequence in both half-decks.
- The equation for that probability is 26! / 20! = 1 : 165,765,600
Notice that the card values, for example jack, queen, king, ace, and the numbers 2 through 9, have no effect on the probability. The uniqueness of low-value cards appearing in a given sequence is the same as the uniqueness of high-value cards appearing in a given sequence.
Summary
This graph shows the dramatic increase in improbability as the number of matching cards increases.
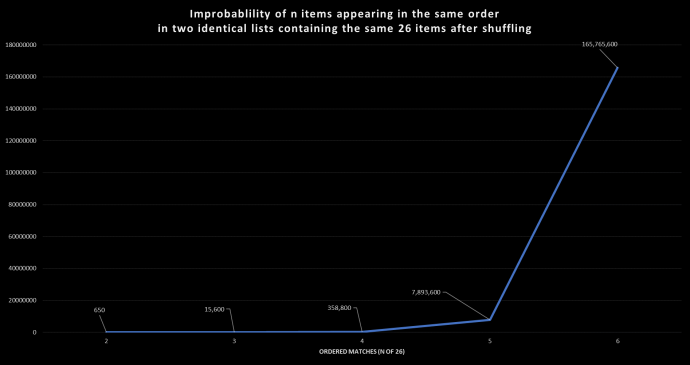
As a point of reference, the odds of 2 people having the same fingerprints is 2.5 times less, or approximately 1:64,000,000! I obtained the information on fingerprint uniqueness from the book entitled Finger Prints (Great Minds) by Francis Galton.
Conclusion
Getting back to comparing software for this court case, I found 26 items that were literal translations of each other in both the plaintiff’s code and the defendant’s code. 6 of these 26 items appeared in the same order in both programs. The probability that this is mere coincidence is so unlikely that it is reasonable to opine that the author of the second program worked from the source code for the first program, which was a trade secret. This constituted a misappropriation of intellectual property.
Thank you.














